二分木探索法

データ探索アルゴリズムの2回目。二分木探索を紹介します。例えば、あらかじめ整列されたデータ

があり、この中から「4」をなるべく少ない回数で探し当てます。その流れは、

1. 「4」とデータの真ん中の値「7」との大小を比較。
2.   4 < 7なので「7」より左のデータ[1, 4, 5]を選ぶ。
3.   [1, 4, 5]の真ん中の値「4」と比較。
4.   4 = 4で一致するので探索終了。

となります。つまり、データを中央の値との大小比較を繰り返して探していきます。上の例だと2回の探索で完了します。

コードを書いてみます。

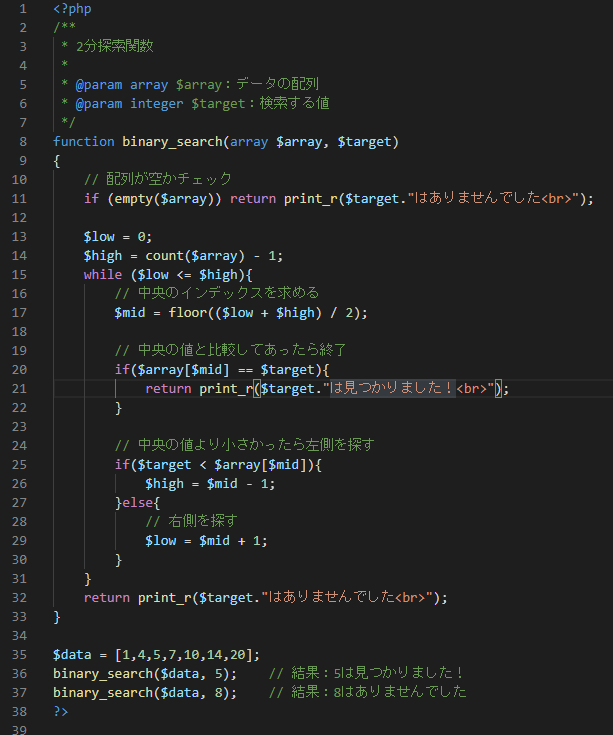
データを半分にしながら探索するので、n個のデータだと平均探索回数はlog2 n 回となります。

だいたい1000個のデータだと10回程度の探索で終わることになり、線形探索法よりもだいぶ処理が速いです。

ただし、データがあらかじめ降順もしくは昇順にソートされていることが前提になるので、

使うときはソートする時間も考慮して使うようにしましょう。